본 자료는 국립 창원대학교 메카트로닉스 공학부 학생을 대상으로 한 공업수학 수업 자료입니다. 본 자료는 수업의 교재인 공업수학I 개정3판 (고형준 외, 도서출판 텍스트북스) 의 내용을 재구성한 것으로 수업보조 자료 이외의 목적이 없음을 알립니다.
직선의 표현
평면상에서 직선의 표현을 공부하는 것은 중학교때일 겁니다. 그때 배운 것은 직선을 알기 위해서는 기울기와 한 점을 알면 된다는 것인데요. 공간상에서도 마찬가지로 방향과 한 점을 알면 됩니다. 그러나 공간이다보니 그 표현이 조금 어려운데요. 이를 벡터를 이용해서 표현할 수 있습니다.
위에서 보면 방금 이야기했던 방향이 벡터a입니다. 그리고 한 점이 벡터r2지요. 위와 같이 표현하면 공간상의 직선을 표현할 수 있습니다.
위 예제에서 세 종류의 답은 모두 같은 직선을 의미합니다. 그런데 위와 같은 표현도 괜찮긴 하지만 또한 매개변수 t를 소거하는 형태로 표현하기도 합니다.
위와 같이 표현하면 분모는 방향벡터의 각 성분이고 분자에는 한 점이 들어가게 되는 것이지요.
평면의 표현
공간상의 평면은
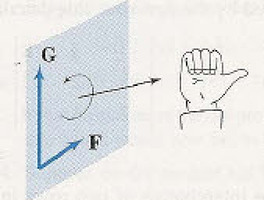
위에서 보다시피 그 평면에 수직한 벡터(법선벡터)와 그 평면 위에 있는 한 점을 알 면 됩니다. 그렇다면 어떤 평면위의 모든 점과 기준이 되는 한 점(r1)으로 만들어진 벡터는 법선벡터와 수직할테니 그 내적은 '0'가 되는 것이지요. 이를 이용해서 평면의 방정식을 도출할 수 있습니다.
참고자료: |
반응형
'Theory > Lecture' 카테고리의 다른 글
| [C/C++] 선택문 (조건문) (6) | 2009.09.02 |
|---|---|
| [공학입문설계] 문제의 정의 및 공학설계 단계 (6) | 2009.09.02 |
| [공업수학] 벡터공간 (6) | 2009.08.30 |
| [공업수학] 벡터의 외적 (10) | 2009.08.30 |
| [공업수학] 벡터의 내적 (4) | 2009.08.30 |
| [공업수학] 벡터의 기초 (4) | 2009.08.30 |
| [선형변환] Convolution 컨볼루션 적분 (8) | 2009.08.30 |








 07 Vector 05.pdf
07 Vector 05.pdf