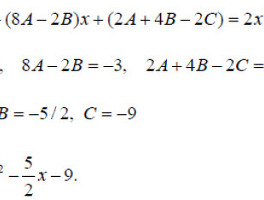선형방정식
위에 동차(homogeneous)와 비동차 방정식의 형태를 보이고 있습니다.
흔히 말하는 미분연산자는 위에서처럼 d/dx를 이야기하는데요
위와 같이 미분을 의미합니다.
위의 표현역시 가능하지요^^
이제
위의 미분방정식에서요.
이미 y1, y2의 해가 밝혀졌다고 하지요. 그러면 선형성(관련글)에 의해
의 형태도 해가 됩니다. 이를 이용하면 비동차방정식의 일반해를 찾는데 큰 도움이 됩니다.
위에서 동차일때의 해과, 특이해의 선형조합의 형태가 전체 일반해가 되거든요.
계수 낮추기
위 문제에서 하나의 해가 y1이라고 해두죠. 다른 해를 u*y1의 형태라고 생각하면
y'와 y''를 구해서 대입해볼 수 있습니다.
그렇게 정리된 식에서 u''와 u'를 줄이기 위해
w를 이용하여, 표현하고 나면, 간단히 1계미방이 되어서 해를 찾을 수 있습니다.
그러면 위와 같이 해를 정의할 수 있겠지요.
위는 2계 미방의 표준형이라고 볼 수 있습니다.
이미 해하나(y1)가 밝혀진 상황에서 방금 예제에서 처럼 정리해나가면
이와같은 결과인데요. 여기서 y1''+Py1'+Qy1은 이미 밝혀진 해(y1)에 의한 표현이니 '0'이 되구요
위의 결과에서 변수분리형으로 표현이 되었으니
간단히 이렇게 공식화가 가능해집니다. 간단한 예를 들면
공식을 적용한 예입니다. 공식으로 푸느냐? 유도하는 과정을 거치느냐? 글쎄요... 개인적인 생각으론 둘다 알면 좋겠다인데요^^
반응형
'Theory > Lecture' 카테고리의 다른 글
| [시스템 시뮬레이션 연재] 1. 라그랑지 방법을 이용한 동역학 모델 구축하기 (28) | 2010.08.09 |
|---|---|
| [공업수학] 미정계수법을 이용한 비동차 방정식의 풀이 (10) | 2010.04.06 |
| [공업수학] 상수계수의 동차선형방정식의 풀이 (4) | 2010.04.06 |
| [공업수학] 1계 미분방정식 (12) | 2010.03.30 |
| [회로이론] RC 회로 (77) | 2010.01.05 |
| [회로이론] 캐패시터 (47) | 2010.01.03 |
| [회로이론] 교류전압과 전류 (2) | 2010.01.01 |














 03-01. 예비이론- 선형방정식.pdf
03-01. 예비이론- 선형방정식.pdf