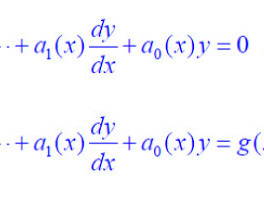변수분리형
1계 미분방정식의 해법은 대체로 정형화되어 이미 정립되어있습니다. 그 방법의 유도과정이나 증명은 공대학생이라면 누구나 가지고 있을 공업수학책이나 각종 인터넷 자료를 참조하시고, 여기서는 몇몇 예제를 통해 풀이만 살펴보도록 하겠습니다.
먼저 위와 같은 형태를 가지는 1계 미방이 있다면, 변수분리형으로 풀 수가 있습니다.
위 예제인데요. 적절히 잘 정리하면 첫 식과 같은 형태로 꾸밀 수 있다는 것을 알 수 있습니다.
이렇게 말이지요.
그리고, 양변을 적분합니다. 그러면, 적분결과를 얻을 수 있고 (물론 적분상수도 나타나겠지요)
위와 같이 정리가 가능해집니다.
이 문제 하나를 더 보죠. 변수분리가 가능하고, y끼리 x끼리 모아서
양변을 적분하면 위의 결과가 나타납니다.
동차형 혹은 비동차형 선형 미분방정식
위와 같이 표현되는 미분방정식 문제에서 f(x)=0라면, 변수분리형으로 풀이가 가능합니다만, 만약 그렇지 않다면 약간은 복잡한 풀이를 가져야합니다. 그러나, 일반화된 풀이법으로 적분인자를 사용하는 방법이 있습니다.
위 예제를 보시면, 애초 첫식에서 P(x)=-3이라고 확인 할 수 있습니다. 이를 이용하면
e^-3x 이라는 적분인자를 찾을 수 있고 이를 원 문제의 양변에 곱하면서 풀이를 시작할 수 있습니다. 관련 과정은 위키디피아의 미분방정식 문서를 확인하시길 바랍니다. 일단 적분인자를 양변에 곱하고 나면,
위와 같이 적분이 가능해집니다.
완전미분방정식
만약
위에서 처럼 두 항이 사실 하나의 미분항으로 표현이 가능할때 완전미분방정식이라고 부릅니다.
즉, 위와 같이 표현될때, 어떤 원래의 식 f(x,y)가 있다면, f를 x에 대해 편미분하면 M이 y에 대해 편미분하면 N으로 표현이 되는 것인데요. 이때 주어진 미분방정식이 완전미방인지 아닌지 판단하는 방법이
위의 식입니다. 일단 완전미분방정식이라는 사실이 밝혀지고 나면 풀이는 쉬워지는데요. 다음 문제를 보겠습니다.
이 문제에서 M=2xy, N=(x^2-1)입니다.
그리고 완전미방인지 확인했더니 맞네요. 그렇다면, 두 식(M, N)을 모두 표현할 수 있는 하나의 식이 있다는 이야기가 됩니다.
그러니 그 원래의 실(f)을 x에 편미분한 결과가 2xy이니까 다시 x에 대해 적분을 수행하는 것입니다.
이렇게 말이죠. 그러면 원래 적분상수같은 애가 하나 남아줘야하는데, 이것을 x에 대한 적분을 수행한것이니 적분상수같은 애는 y로만 된 어떤 함수(g(y))라고 생각을 해야합니다.
그리고, 다시 y에대해 편미분을 하면, x^2-1과 같아야할 테니..
g'가 -1이라는 것을 알 수 있는 것이지요.
그러면, g는 -y라고 생각할 수 있습니다. 이때 또 적분상수에 대한 의문이 들텐데 여기서 잡아도 되고 최종식에서 잡아도 무리는 없습니다.
이렇게 해서 풀이를 완료할 수 있네요^^
반응형
'Theory > Lecture' 카테고리의 다른 글
| [공업수학] 미정계수법을 이용한 비동차 방정식의 풀이 (10) | 2010.04.06 |
|---|---|
| [공업수학] 상수계수의 동차선형방정식의 풀이 (4) | 2010.04.06 |
| [공업수학] 선형방정식 (12) | 2010.03.30 |
| [회로이론] RC 회로 (77) | 2010.01.05 |
| [회로이론] 캐패시터 (47) | 2010.01.03 |
| [회로이론] 교류전압과 전류 (2) | 2010.01.01 |
| [회로이론] 직병렬회로 (14) | 2009.12.30 |















 02. First-Order Differential Equations.pdf
02. First-Order Differential Equations.pdf