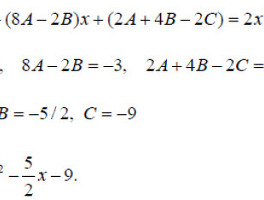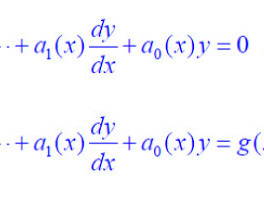[공업수학] 상수계수의 동차선형방정식의 풀이

동차선형방정식의 일반적이 해

지난번 글에서 1계 선형미방

의 해의 형태가 위와 같다는 것을 이야기했습니다. 동차미방의 한 해가 지수의 형태를 가진다는 것을 알았으니

e^mx의 해를 다시 대입해서 정리하면 위와 같습니다. 이때, 지수가 '0'이 될 수 없을테니 2계선형미방의 경우 곱해져있는 다항식이 '0'이 되는 것은 당연할 것이고, 그것은 간단히 근의 공식으로 해결할 수 있습니다. 

서로 다른 실근을 가지는 경우

서로 다른 실근을 가진다면 해의 형태는 위와 같습니다. 이를 확인하는 것은 다시 대입하면 간단히 확인 가능합니다. 

위 2계 동차 선형 미분방정식을 다항식의 형태로 표현하면

이렇게 되고 그 해는

이고 다시 해의 일반적 형태에 대입하면

해를 구할 수 있게 됩니다.

중근을 가지는 경우

중근

을 가지는 경우는 이전에 미분방정식의 차수낮추기에서 이야기한 형태로 두번째 해를 잡아 볼 수 있습니다.

위 예제에서

중근이 나타나게 되고 역시 첫 식에 적용하여 해를 구할 수 있게 됩니다.

허근을 가지는 경우

허근을 가지는 경우는

이렇게 두 실근을 가지는 경우처럼 잡아 줄 수 있는데요. 흔히 오일러공식으로 알려져 있는

이 식을 이용해서

로 정리하고

연립해서 표현가능하니까 허근의 경우는

로 해를 생각하게 됩니다.

위 예제에서

이렇게 적용가능하지요.

참고자료 03-03.pdf