라플라스 변환
위에 라플라스변환의 정의가 나타나 있습니다.
라플라스변환의 정의를 이용해서 "1"을 라플라스변환한 결과입니다. 그러나, 위 정의식을 계속 사용한다는 것은 뭐 힘든일이겠지요^?^. 그래서
저와 같이 변환표를 이용합니다.
라플라스 역변환
위는 라플라스 역변환표입니다. 뭐 당연히 라플라스 변환표의 반대겠지요^^. 라플라스 역변환의 정의는 아주 복잡해서 손으로 푸는 것은 어렵습니다. 그래서 위 역변환표에 가장 가까운 형태로 식의 형태로 바꾸어가는 겁니다.
위의 예제를 보면 무슨 말인지 알 수 있을겁니다.
위 예제는 항별나누기를 이용해서 식을 분리하고, 라플라스 변환이 가지는 선형성을 이용해서 각각을 역변환하는 것입니다.
위 예제는 흔히 말하는 유수정리(Residue Theorem)의 부분분수 전개를 이용한 것입니다. 보통은 위 전개방식은 분모를 영으로 만드는 것을 대입한다고 외웁니다.^^.
이 라플라스 변환과 역변환은 미방의 풀이에 큰 장점을 가지게 되는데요 일단 도함수를 변환하면 위 정리와 같습니다.
미방을 라플라스 변환하고 대수방정식화된 식의 해를 찾고 다시 역변환하는 과정을 거치게 됩니다.
위 간단한 예를 보면
위와 같이 초기값을 고려하여 라플라스변환하고 라플라스변환된 식을 푼다음 다시 역변환으로 그 해를 찾는 것입니다.
Translation Theorem
시간영역에서 지수함수는 라플라스 변환을 하고 나면 단순 평행이동이 되어있습니다.
이를 이용하면 위 예제들 역시 간단히 그 해를 찾을 수 있습니다.
Derivatives of Transforms
시간영역에서 시간의 급수형태의 함수를 라플라스변환하면 라플라스 도메인 영역에 대한 미분형태로 나타나게 됩니다.
'Theory > Lecture' 카테고리의 다른 글
| [공업수학] 역행렬 (Inverse Matrix) (18) | 2009.09.23 |
|---|---|
| [공업수학] 행렬식 determinant (4) | 2009.09.14 |
| [공업수학] 행렬의 기초 (12) | 2009.09.07 |
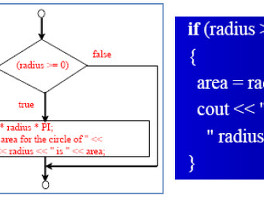
| [C/C++] 선택문 (조건문) (6) | 2009.09.02 |
| [공학입문설계] 문제의 정의 및 공학설계 단계 (6) | 2009.09.02 |
| [공업수학] 벡터공간 (6) | 2009.08.30 |
| [공업수학] 벡터를 이용한 직선과 평면의 표현 (4) | 2009.08.30 |



 Laplace Transform -1.pdf
Laplace Transform -1.pdf